各種のランキングをRでためしてみよう(1)—隣接行列と原始的なPageRank

前エントリにひきつづき、研究のための体制立て直しの様子を、垂れ流していきたいと思います！

隣接行列

こんどは隣接行列 (adjacency matrix) からグラフをつくる。前エントリでみたRion778さんのページを、ひきつづき参考にします。

graph.adjacency()関数により，隣接行列 (adjacency matrices) からグラフオブジェクトを作成できる．対角成分が0でなければループになる．

そこでまず、

> n <- c(
 + 0,1,0,0,0,0,
 + 0,0,1,1,0,0,
 + 0,0,0,0,0,0,
 + 0,0,1,0,0,1,
 + 0,0,0,1,0,0,
 + 0,0,0,0,0,0)
> n <- t(matrix(n, nrow=6))
> n
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    0    1    0    0    0    0
[2,]    0    0    1    1    0    0
[3,]    0    0    0    0    0    0
[4,]    0    0    1    0    0    1
[5,]    0    0    0    1    0    0
[6,]    0    0    0    0    0    0

という行列nを手入力した(ほんとはCSVファイルなどからも読めたはずなので、実際にはこのようなやりかたは、何度もデータを換えて実験するときには、あまりおすすめしないが)。

graph.adjacency {igraph} R Documentation
Create graphs from adjacency matrices
...
Usage
graph.adjacency(adjmatrix, mode=c("directed", "undirected", "max",
"min", "upper", "lower", "plus"), weighted=NULL, diag=TRUE,
add.colnames=NULL, add.rownames=NA)

>  plot(graph.adjacency(n))

ここで「あ、ちげえ。plotして気づいたけど、nが隣接行列の転置になってるじゃん！」……などと、いうこともある(直した)。

Hofuku, Oshima "Measures to Represent the Proparties of Nodes in a Drected Graph"(あれ未発表？そういえば、これ書いてだいじょぶか？).
この論文のあつかうもの:

以降、この論文と同じ実験をRでやって同じ結果が得られるかをみます。
とりあえず、きょうはPageRankのかんたんなやつを。

追記:

いまさら「RでPageRank」とかググったら、igraph内に、そのものすばりgraph.rankというものが…。

Calculates the Google PageRank for the specified vertices.
Usage
page.rank (graph, vids = V(graph), directed = TRUE, damping = 0.85,
weights = NULL, options = igraph.arpack.default)
page.rank.old (graph, vids = V(graph), directed = TRUE, niter = 1000,
eps = 0.001, damping = 0.85, old = FALSE)

ぎゃふん！

原始的なPageRank

元祖のPageRankやります。
このPageRankは「よいページからリンクされているページはよいページである。」みたいに、リンクを単純な相互評価としてとらえる仮説に基づいて、みんなの意見を統一したような評価を得るモデルです。訪問者数のある種の期待値ともいえるそうな。
参照してる論文の書き方、どうも少し特殊な気がするので、少しはしょって書くけど。

ソース全体はこんな感じ。

n <- c(
0,1,0,0,0,0,
0,0,1,1,0,0,
0,0,0,0,0,0,
0,0,1,0,0,1,
0,0,0,1,0,0,
0,0,0,0,0,0)
n <- t(matrix(n, nrow=6))

p<-n
p[rowSums(p)==0,]<-1
p<-p/rowSums(p)

pp<-0.1*(1/6)+0.9*p
q<-t(pp)

r<-vector("numeric",6)
r[]<-1/6
for(i in 1:10)r<<-q%*%r
r

以下、詳細。

STEP1＆STEP2(規格化):

各行のl1-ノルム(この場合、単純な合計)に関して、1になるように調整する(各行を、おのおののl1-ノルムで割る)(STEP1)。
ただし、いきなりn/rowSums(n)とやりたくなるが、これだとゼロ割りしてやっかいなので、~~合計がゼロのとこだけ1で割るようにしておきます(3行目)~~ぜんぶゼロの行はまず非ゼロの、適当な値を一律に入れてしまう(STEP2)。

ちなみに、以前、参考にした論文も:

Amy N. Langville, Carl D. Meyer 'A Survey of Eigenvector Methods for Web Information Retrieval', SIAM REVIEW c Vol. 47, No. 1, pp. 135–161 (Society for Industrial and Applied Mathematics, 2005).
- http://meyer.math.ncsu.edu/Meyer/PS_Files/Survey.pdf
- HITS、PageRank、SALSAとか「絶対値最大の固有値に対する固有ベクトル」をランキング指標として使う方面の手法の、まとめ。べき乗法、ペロン=フロベニウスの定理とか、そんな感じ。
同じ著者による本の日本語版もある
- Google PageRankの数理 ―最強検索エンジンのランキング手法を求めて―
  - 作者: Amy N.Langville,Carl D.Meyer,岩野和生,黒川利明,黒川洋
  - 出版社/メーカー: 共立出版
  - 発売日: 2009/10/10
  - メディア: 単行本
  - 購入: 4人クリック: 249回
  - この商品を含むブログ (23件) を見る

これによると、ゼロの行にいれるのは、「 $\bf{e}^T/n$ 、ただしnはPのオーダー」だそうな。具体的にはよくわかんないので1/n(=1/6)にしておく。これをpとする(よく考えたら、各行の合計が1にならないとまずいのです)。

> p<-n
> tmp<-rowSums(n)
> p[tmp==0,]<-1
> tmp[tmp==0]<-6
> p<-p/tmp
> p
          [,1]      [,2]      [,3]      [,4]      [,5]      [,6]
[1,] 0.0000000 1.0000000 0.0000000 0.0000000 0.0000000 0.0000000
[2,] 0.0000000 0.0000000 0.5000000 0.5000000 0.0000000 0.0000000
[3,] 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667
[4,] 0.0000000 0.0000000 0.5000000 0.0000000 0.0000000 0.5000000
[5,] 0.0000000 0.0000000 0.0000000 1.0000000 0.0000000 0.0000000
[6,] 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667

STEP3(べき乗法を収束させる条件):

行列pをともかく既約にする(グラフを強連結にする)ために、
$\bf{P'}_1=(1-c)\frac{1}{n}\bf{E}+c\bf{P}_1$
みたいなことをする。ただし、Eは全要素が1で、c=0.9とする。Rでは右辺をp、左辺はppと書いている。
(いちおう、より一般的に $\bf{E} = \bf{e}\bf{v}^T$ であるEを用いて、vを動かしてもっと細かく制御する方法もあるらしい。けど、めんどいのでやりません。)

> pp<-0.1*(1/6)+0.9*p
> pp
           [,1]       [,2]       [,3]       [,4]       [,5]       [,6]
[1,] 0.01666667 0.91666667 0.01666667 0.01666667 0.01666667 0.01666667
[2,] 0.01666667 0.01666667 0.46666667 0.46666667 0.01666667 0.01666667
[3,] 0.04166667 0.04166667 0.04166667 0.04166667 0.04166667 0.04166667
[4,] 0.01666667 0.01666667 0.46666667 0.01666667 0.01666667 0.46666667
[5,] 0.01666667 0.01666667 0.01666667 0.91666667 0.01666667 0.01666667
[6,] 0.04166667 0.04166667 0.04166667 0.04166667 0.04166667 0.04166667
> q<-t(pp)

転置したものをqという。これの最大固有値は1になっているはずで、べき乗法によりこれに対する固有ベクトルが求まるはず。

STEP4(べき乗法で固有ベクトル):

> r<-vector("numeric",6)
> r[]<-1/6
> r<-q%*%r
> r
           [,1]
[1,] 0.06666667
[2,] 0.21666667
[3,] 0.21666667
[4,] 0.29166667
[5,] 0.06666667
[6,] 0.14166667
> r<-q%*%r
> r
           [,1]
[1,] 0.07041667
[2,] 0.13041667
[3,] 0.29916667
[4,] 0.22791667
[5,] 0.07041667
[6,] 0.20166667
> r<-q%*%r
> r
           [,1]
[1,] 0.09179167
[2,] 0.15516667
[3,] 0.25304167
[4,] 0.21385417
[5,] 0.09179167
[6,] 0.19435417
> r<-q%*%r
> r
           [,1]
[1,] 0.08377604
[2,] 0.16638854
[3,] 0.24983542
[4,] 0.23621354
[5,] 0.08377604
[6,] 0.18001042
> r<-q%*%r
> r
           [,1]
[1,] 0.08114354
[2,] 0.15654198
[3,] 0.26231448
[4,] 0.23141682
[5,] 0.08114354
[6,] 0.18743964
> r<-q%*%r
> r
           [,1]
[1,] 0.08412978
[2,] 0.15715897
[3,] 0.25871124
[4,] 0.22760286
[5,] 0.08412978
[6,] 0.18826735
> r<-q%*%r
> r
           [,1]
[1,] 0.08371346
[2,] 0.15943026
[3,] 0.25685628
[4,] 0.23015180
[5,] 0.08371346
[6,] 0.18613474

と、まあこんな感じか。7回ですか。

左を一位として、ノードの番号を表示してみると

> order(r,decreasing=TRUE)
[1] 3 4 6 2 1 5

となる(1と5はタイ)。
さっきも見た画像ですが、これに「重要なノードからのエッジがあるノードは重要である」というモデルを適用すると、こういう順番になるわけです。

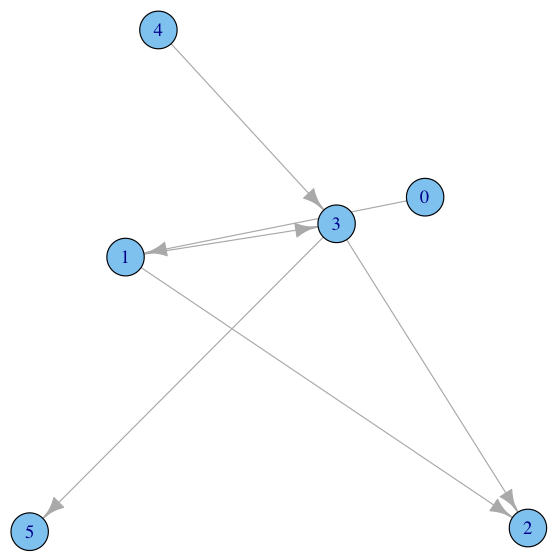
ちなみに、何度「r<<-q%*%r」を繰り返しても

> sum(r)
[1] 1

になってるはずで、実際
「0.08371346+0.15943026+0.25685628+0.23015180+0.08371346+0.18613474=1」です。
これははじめに行列の各行のl1-ノルム(合計)が1になるように規格化したからです。また「絶対値最大の固有値が1だ」ということとも関連している。上記の無限の繰り返しによって得られたものが、そのqの固有値1に対する固有ベクトル。

あと、増える要素は単調に増えるし、減る方も同様(たぶん)。なので、エネルギー保存則みたいなものというか、そういう感じですたぶん。要素がすべて正の実数の既約な行列の、絶対値最大の固有値がべき乗法で求まることのの保証とかは、ペロンさんとフロベニウスさんにお聞きください。

余談

で、いまさらだけど、じつはRにはeigenという関数があって、行列のサイズが小さければ

> eigen(cbind(c(1,-1),c(-1,1)))
$values
[1] 2 0

$vectors
           [,1]       [,2]
[1,] -0.7071068 -0.7071068
[2,]  0.7071068 -0.7071068

みたいに一行で求まります。べき乗法の必要がない、ふつうの場合はたぶんこちらを使います。

とかいって、でも固有ベクトルが一致しないんですよね、なぜか…。

>  eigen(q)
$values
[1]  1.000000e+00+0.000000e+00i -1.789082e-01+4.677976e-01i
[3] -1.789082e-01-4.677976e-01i -2.421836e-01+0.000000e+00i
[5]  3.801593e-09+0.000000e+00i -3.801593e-09+0.000000e+00i

$vectors
              [,1]                  [,2]                  [,3]
[1,] -0.1896813+0i -0.1616564-0.1997846i -0.1616564+0.1997846i
[2,] -0.3603945+0i -0.3932094+0.1997846i -0.3932094-0.1997846i
[3,] -0.5870163+0i  0.5548659+0.0000000i  0.5548659+0.0000000i
[4,] -0.5225721+0i -0.0993472+0.4656472i -0.0993472-0.4656472i
[5,] -0.1896813+0i -0.1616564-0.1997846i -0.1616564+0.1997846i
[6,] -0.4248388+0i  0.2610036-0.2658626i  0.2610036+0.2658626i
              [,4]             [,5]             [,6]
[1,] -0.1861799+0i  2.515346e-16+0i -2.355139e-16+0i
[2,]  0.5056998+0i  1.194726e-08+0i  1.194725e-08+0i
[3,] -0.3195199+0i  7.071068e-01+0i -7.071068e-01+0i
[4,] -0.4339382+0i -5.973627e-09+0i -5.973629e-09+0i
[5,] -0.1861799+0i -5.973627e-09+0i -5.973628e-09+0i
[6,]  0.6201181+0i -7.071068e-01+0i  7.071068e-01+0i